Answer:
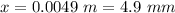

Step-by-step explanation:
Given:
- mass of the object,
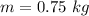
- elastic constant of the connected spring,
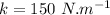
- coefficient of static friction between the object and the surface,
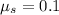
(a)
Let x be the maximum distance of stretch without moving the mass.
The spring can be stretched up to the limiting frictional force 'f' till the body is stationary.
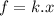

where:
N = m.g = the normal reaction force acting on the body under steady state.
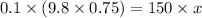
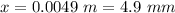
(b)
Now, according to the question:
- Amplitude of oscillation,

- coefficient of kinetic friction between the object and the surface,
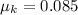
Let d be the total distance the object travels before stopping.
Now, the energy stored in the spring due to vibration of amplitude:
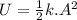
This energy will be equal to the work done by the kinetic friction to stop it.
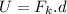
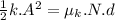
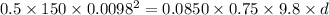

is the total distance does it travel before stopping.