Answer:
Area = 2500 square feet is the largest area enclosed
Explanation:
A rectangular piece of land borders a wall. The land is to be enclosed and to be into divided 3 equal plots with 200 feet of fencing
Let x be the length of each box and y be the width of the box
Perimeter of the box= 3(length ) + 4(width)
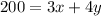
solve for y
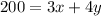
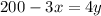
divide both sides by 4
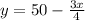
Area of the rectangle = length times width
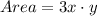
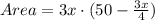
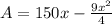
Now take derivative
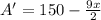
Set it =0 and solve for x
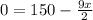
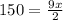
multiply both sides by 2/9
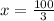
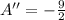
For any value of x, second derivative is negative
So maximum at x= 100/3
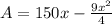 , replace the value of x
, replace the value of x
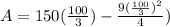
Area = 2500 square feet is the largest area enclosed