Question

A rectangular piece of land borders a wall. The land is to be enclosed and to be into divided 3 equal plots with 200 feet of fencing. What is the largest area that can be enclosed?

Answer 1

Area = 2500 square feet is the largest area enclosed

Explanation:

A rectangular piece of land borders a wall. The land is to be enclosed and to be into divided 3 equal plots with 200 feet of fencing

Let x be the length of each box and y be the width of the box

Perimeter of the box= 3(length ) + 4(width)

`200=3x+4y`

solve for y

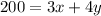
`200=3x+4y`

`200-3x=4y`

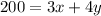
divide both sides by 4

`y=50-(3x)/(4)`

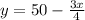
Area of the rectangle = length times width

`Area = 3x \cdot y`

`Area = 3x \cdot (50-(3x)/(4))`

`A=150x-(9x^2)/(4)`

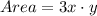
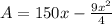
Now take derivative

`A'=150-(9x)/(2)`

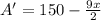
Set it =0 and solve for x

`0=150-(9x)/(2)`

`150=(9x)/(2)`

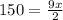
multiply both sides by 2/9

`x=(100)/(3)`

`A''=-(9)/(2)`

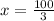
For any value of x, second derivative is negative

So maximum at x= 100/3

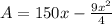`A=150x-(9x^2)/(4)` , replace the value of x

`A=150((100)/(3))-(9((100)/(3))^2)/(4))`

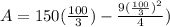
Area = 2500 square feet is the largest area enclosed