Question

I need help with this homogeneous equation


`(dy)/(dx) = (x^(2)+y^(2) )/(2xy)`

Answer 1

`ln [1 - ((y)/(x) )^(2) ] + ln x + c = 0`. This is the solution.

Explanation:

The homogeneous differential equation is given by

`(dy)/(dx) = (x^(2) + y^(2) )/(2xy)`

⇒
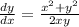
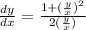`(dy)/(dx) = (1 + ((y)/(x) )^(2) )/(2((y)/(x) ))` ........ (1)

Now to solve this differential equation we assume that y = vx where v is another variable.

So, differentiating with respect to x we get
`(dy)/(dx) = v + x (dv)/(dx)`

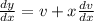
Therefore, the above equation (1) becomes

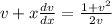`v + x (dv)/(dx) = (1 + v^(2) )/(2v)` {Since
`v = (y)/(x)`}

⇒
`x(dv)/(dx) = (1 + v^(2) - 2v^(2)  )/(2v)`

⇒
`x(dv)/(dx) = (1 - v^(2))/(2v)`

⇒
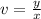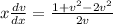
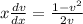
`(2v)/(1 - v^(2) ) dv = (dx)/(x)` {By separation of variables}

Now, integrating both sides we get,

`\int {(2v)/( 1- v^(2))} \, dv = \int {(dx)/(x) } \, dx`

⇒
`- \int {(d(1 - v^(2) ))/(1 - v^(2))}  = \int {(dx)/(x) }`

⇒
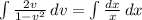
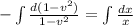
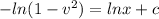`- ln (1 - v^(2)) = ln x + c` {Where c is the integration constant}

⇒
`ln [1 - ((y)/(x) )^(2) ] + ln x + c = 0` (Answer)