Question

The surface of a hill is modeled by z = 100 − 4 x 2 − 2 y 2 . When a group of hikers reach the point (-3,-2,56) it begins to snow. They decide to descend the hill as rapidly as possible. Which of the following vectors points in the direction they should start their descent? < 24 , 8 > < 24 x , 8 y > < − 24 x , − 8 y > < − 24 , − 8 > None of the above

Answer 1

(-24, -8)

Explanation:

Let us recall that when we have a function f

`\large f:\mathbb{R}^2\rightarrow \mathbb{R}\\f(x,y)=z`

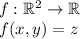
if the gradient of f at a given point (x,y) exists, then the gradient of f at this point (x,y) gives the direction of maximum rate of increasing and minus the gradient of f at this point gives the direction of maximum rate of decreasing. That is

`\large \\abla f=((\partial f)/(\partial x),(\partial f)/(\partial y))`

at the point (x,y) gives the direction of maximum rate of increasing

`\large -\\abla f`

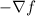
at the point (x,y) gives the direction of maximum rate of decreasing

In this case we have

`\large f(x,y)=100-4x^2-2y^2`

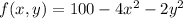
and we want to find the direction of fastest speed of decreasing at the point (-3,-2)

`\large \\abla f(x,y)=(-8x,-4y) \Rightarrow -\\abla f=(8x,4y)`

at the point (-3,-2) minus the gradient equals

`\large -\\abla f(-3,-2)=(-24,-8)`

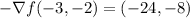
hence the vector (-24,-8) points in the direction with the greatest rate of decreasing, and they should start their descent in that direction.