Question

The hollow tube is pivoted about a horizontal axis through point O and is made to rotate in the vertical plane with a constant counterclockwise angular velocity = 2.9 rad/sec. If a 0.15-lb particle is sliding in the tube toward O with a velocity of 4.8 ft/sec relative to the tube when the position θ = 36° is passed, calculate the magnitude N of the normal force exerted by the wall of the tube on the particle at this instant.

Answer 1

To solve the problem it is necessary to apply the concepts related to Newton's second law, as well as to the sum of forces in this type of bodies.

According to the description I make a diagram that allows a better understanding of the problem.

Performing sum of forces in the angular direction in which it is inclined we have to

`\sum F = ma_(\theta)`

`N - W cos\theta = ma_(\theta)`

`N = ma_(\theta)+Wcos\theta`

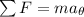
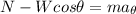
Tangential acceleration can be expressed as

`a_(\theta) = (r\ddot{\theta}+2\dot{r}\dot{\theta})`

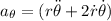
Our values are given by,

`\dot{\theta} = 2.9rad/s`

`m = 0.15 lb`

`\theta = 36\°`

`v = 4.8ft/s`

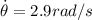
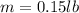
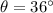
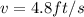
Substituting
`\ddot{\theta}=0rad/s^2 ,  \dot{r}=-4.8ft/s, \dot{\theta}=2.9 rad/s`

`a_(\theta) = r*0+2*(4.8*2.9)\\a_(\theta)=27.84ft/s^2`

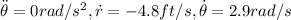
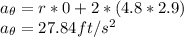
At the same time we acan calculate the mass of the particle, then

W = mg

Where,

W = Weight of the particle

m = mass

g = acceleration due to gravity

`0.15lb = m(32.2ft/s^2)`

`m = 4.66*10^(-3)Lb`

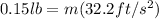
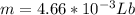
Now using our first equation we have that

`N = ma_(\theta)+Wcos\theta`

`N = (4.66*10^(-3))(27.84)+0.2cos36`

`N = 0.2914Lb`

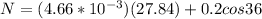
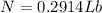
Therefore the normal force exerted by the wall of the tube on the particle at this instant is 0.2914Lb