To solve this exercise it is necessary to take into account the concepts related to the magnetic field and its vector representation through the cross product or vector product.
According to the definition the direction of the electromagnetic wave propagation is given by
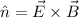
Where,
E = Electric Field
B = Magnetic Field
According to the information provided, the direction of propagation of the electromagnetic wave is on the X axis, which for practical purposes we will denote as
 , on the other hand it is also indicated that the magnetic field is in the Y direction, that for practical purposes we will denote it as
, on the other hand it is also indicated that the magnetic field is in the Y direction, that for practical purposes we will denote it as
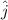 . In this way using the previous equation we would have to,
. In this way using the previous equation we would have to,
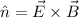
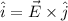
The cross product identity is
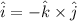
From the equation we can notice that the electric field would be given by,
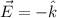
Therefore the direction of electric field is negative z-axis.