Final answer:
The demand for tie-dyed T-shirts will drop by approximately 23 T-shirts when the price is increased from $15 to $17. This calculation is based on the function q = 510 − 90
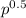 , which represents the demand in relation to the price.
, which represents the demand in relation to the price.
Step-by-step explanation:
The student is asking how fast the demand for tie-dyed T-shirts will drop if the price increases by $2 when the demand is represented by the function q = 510 − 90
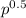 . Since the current price is $15, we need to calculate the demand at both $15 and $17 to find the rate of change in demand when the price is raised by $2.
. Since the current price is $15, we need to calculate the demand at both $15 and $17 to find the rate of change in demand when the price is raised by $2.
To find the demand at the current price of $15, substitute p = 15 into the demand function:
q = 510 − 90
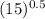
q = 510 − 90(3.87)
q = 510 − 348.3
q = 161.7
To find the demand when the price is $17, substitute p = 17 into the demand function:
q = 510 − 90
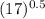
q = 510 − 90(4.12)
q = 510 − 371
q = 139
The change in demand is the difference between the two quantities:
Δq = 161.7 - 139 = 22.7
The demand drops by approximately 23 T-shirts when the price increases by $2.