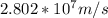Question

Two particles of equal masses (m = 5.5x10-15 kg) are released from rest with a distance between them is equal to 1 m. If particle A has a charge of 12 μC and particle B has a charge of 60 μC, what is the speed of particle B at the instant when the particles are 3m apart?

Answer 1

To solve this problem it is necessary to resort to the energy conservation equations, both kinetic and electrical.

By Coulomb's law, electrical energy is defined as

`EE = (kq_1q_2)/(d)`

Where,

EE = Electrostatic potential energy

q= charge

d = distance between the charged particles

k = Coulomb's law constant

While kinetic energy is defined as

`KE = (1)/(2) mv^2`

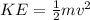
Where,

m= mass

v = velocity

There by conservation of energy we have that

EE= KE

There is not Initial kinetic energy, then

`(kq_1q_2)/(d)-(kq_1q_2)/(d') = 2*(1)/(2)mv_f^2`

`(kq_1q_2)/(d)-(kq_1q_2)/(d') = mv_f^2`

`v_f^2= ((kq_1q_2)/(d)-(kq_1q_2)/(d') )/(m)`

`v_f = \sqrt{((kq_1q_2)/(d)-(kq_1q_2)/(d'))/(m)}`

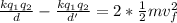
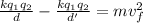
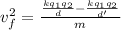
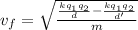
Replacing with our values we have,

`v_f = \sqrt{(((9*10^9)(12*10^(-6))(60*10^(-6)))/(1)-((9*10^9)(12*10^(-6))(60*10^(-6)))/(3))/(5.50*10^(-15))}`

`v_f = 2.802*10^7m/s`

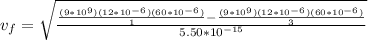
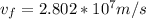
Therefore the speed of particle B at the instat when the particles are 3m apart is
`2.802*10^7m/s`