Question

on dividing $200 between A and B such that twice of A's share is less than 3 times than B's share by $20

Answer 1

Share of A is $116 and Share of B is $84.

Explanation:

Let the share of A be
`x`

Let the share of B be
`y`

Given:

$200 is shared between A and B

So,
`x+y =\$200\ \ \ \ equation \ 1`

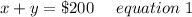
Also given;

twice of A's share is less than 3 times than B's share by $20

`2x= 3y -20\\2x-3y = -20 \ \ \ \ equation \ 2`

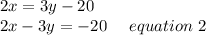
Solution:

Now multiplying equation 1 by 3 we get,

`3x+3y=600 \ \ \ \ equation \ 3`

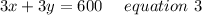
Now Adding equation 2 and equation 3 we get

`(2x-3y = -20)+ (3x+3y=600)\\5x=580\\\\x=(580)/(5)=\$116`

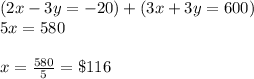
Now Substituting the value of x in equation 1 we get,

`x+y=200\\116+y=200\\y=200-116 = \$84`

Hence, Share of A is $116 and Share of B is $84.