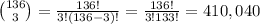Question

A major software company is arranging a job fair with the intention of hiring 6 recent graduates. The 6 jobs are different, and numbered 1 through 6. No candidate can receive more than one offer. In response to the company's invitation, 136 candidates have appeared at the fair. a. How many ways are there to extend the 6 offers to 6 of the 136 candidates? {1 point} b. How many ways are there to extend the 6 offers to 6 of the 136 candidates, if we already know that Computer Joe is getting an offer, but we do not know which? {1 point} C. How many ways are there to extend the 6 offers to 6 of the 136 candidates, if we already know that Computer Joe is getting an offer for job number 2? {1 point} d. How many ways are there to extend the 6 offers to 6 of the 136 candidates, if we already know that Computer Joe is not getting any offers? {1 point} e. How many ways are there for 3 interviewers to select 3 resumes (one resume for each interviewer) from the pile of 136 resumes for the first interview round?

Answer 1

a) 7,858,539,612

b) 2,080,201,662

c) 346,700,277

d) 7,511,839,335

e) 410,040

Explanation:

a. How many ways are there to extend the 6 offers to 6 of the 136 candidates?

Combinations of 136 (candidates) taken 6 (offers) at a time without repetition:

`\large \binom{136}{6}=(136!)/(6!(136-6)!)=(136!)/(6!130!)=7,858,539,612`

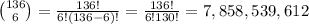
b. How many ways are there to extend the 6 offers to 6 of the 136 candidates, if we already know that Computer Joe is getting an offer, but we do not know which?

There are 6 ways Computer Joe can get an offer. Now there are left 5 offers and 135 candidates. So there are

6 times combinations of 135 taken 5 at a time without repetition:

`\large 6*\binom{135}{5}=6*(135!)/(5!(135-5)!)=6*(135!)/(5!130!)=2,080,201,662`

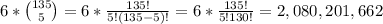
c. How many ways are there to extend the 6 offers to 6 of the 136 candidates, if we already know that Computer Joe is getting an offer for job number 2?

Now, we only have 5 offers and 135 candidates. So there are combinations of 135 taken 5 at a time without repetition:

`\large \binom{135}{5}=(135!)/(5!(135-5)!)=(135!)/(5!130!)=346,700,277`

d. How many ways are there to extend the 6 offers to 6 of the 136 candidates, if we already know that Computer Joe is not getting any offers?

Here we have 6 offers and 135 candidates, given that Computer Joe is out. So there are combinations of 135 taken 6 at a time without repetition:

`\large \binom{135}{6}=(135!)/(6!(135-6)!)=(135!)/(6!129!)=7,511,839,335`

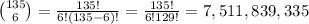
e. How many ways are there for 3 interviewers to select 3 resumes (one resume for each interviewer) from the pile of 136 resumes for the first interview round?

There are combinations of 136 taken 3 at a time without repetition:

`\large \binom{136}{3}=(136!)/(3!(136-3)!)=(136!)/(3!133!)=410,040`