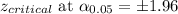Answer:
Confidence interval: (1760,1956)
Explanation:
We are given the following information in the question:
Sample size, n = 81
Sample mean =
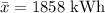
Population standard deviation =
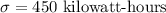
Confidence Level = 95%
Significance level = 5% = 0.05
Confidence interval:
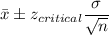
Putting the values, we get,