Answer:
A. positive slope.
Explanation:
In the least square linear regression of Y on X, the straight line of best fit is given by,
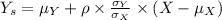 ------------------(1)
------------------(1)
[where
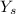 is the estimated value of Y]
is the estimated value of Y]
Clearly, here,
Slope pf the line =
 ---------------------------------(2)
---------------------------------(2)
Y- intercept =
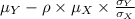 -----------------(3)
-----------------(3)
and,
X - intercept =
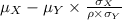 ----------------(4) [putting
----------------(4) [putting
 in (1) and taking the value of X]
in (1) and taking the value of X]
So,
since

[since
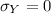 or
or
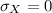 will result in a degenerate distribution, hence these cases are discarded]
will result in a degenerate distribution, hence these cases are discarded]
so, correlation coefficient =
 > 0 implies
> 0 implies
A. positive slope. [as evident from (1)]
clearly from (3) and (4) all the other options are false.