Question

A car moving at 10.0 m/s encounters a depression in the road that has a circular cross-section with a radius of 30.0 m. What is the normal force exerted by the seat of the car on a 60.0-kg passenger when the car is at the bottom of the depression?a. 200 Nb. 389 Nc. 789 Nd. 589 N

Answer 1

F = 789 Newton

Step-by-step explanation:

Given that,

Speed of the car, v = 10 m/s

Radius of circular path, r = 30 m

Mass of the passenger, m = 60 kg

To find :

The normal force exerted by the seat of the car when the it is at the bottom of the depression.

Solution,

Normal force acting on the car at the bottom of the depression is the sum of centripetal force and its weight.

`N=mg+(mv^2)/(r)`

`N=m(g+(v^2)/(r))`

`N=60* (9.81+((10)^2)/(30))`

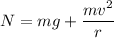
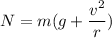
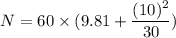
N = 788.6 Newton

N = 789 Newton

So, the normal force exerted by the seat of the car is 789 Newton.