Question

Find the work required to move an object in the force field F = ex+y <1,1,z> along the straight line from A(0,0,0) to B(-1,2,-5). Also, deternine if the force is conservative.

Find the work required to move an object in the fo

Answer 1

Work = e+24

F is not conservative.

Explanation:

To find the work required to move an object in the force field

`\large F(x,y,z)=(e^(x+y),e^(x+y),ze^(x+y))`

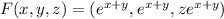
along the straight line from A(0,0,0) to B(-1,2,-5), we have to parameterize this segment.

Given two points P, Q in any euclidean space, you can always parameterize the segment of line that goes from P to Q with

r(t) = tQ + (1-t)P with 0 ≤ t ≤ 1

so

r(t) = t(-1,2,-5) + (1-t)(0,0,0) = (-t, 2t, -5t) with 0≤ t ≤ 1

is a parameterization of the segment.

the work W required to move an object in the force field F along the straight line from A to B is the line integral

`\large W=\int_(C)Fdr`

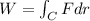
where C is the segment that goes from A to B.

`\large \int_(C)Fdr =\int_(0)^(1)F(r(t))\circ r'(t)dt=\int_(0)^(1)F(-t,2t,-5t)\circ (-1,2,-5)dt=\\\\=\int_(0)^(1)(e^t,e^t,-5te^t)\circ (-1,2,-5)dt=\int_(0)^(1)(-e^t+2e^t+25te^t)dt=\\\\\int_(0)^(1)e^tdt-25\int_(0)^(1)te^tdt=(e-1)+25\int_(0)^(1)te^tdt`

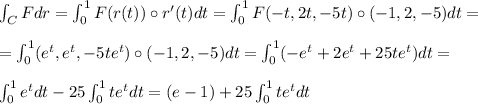
Integrating by parts the last integral:

`\large \int_(0)^(1)te^tdt=e-\int_(0)^(1)e^tdt=e-(e-1)=1`

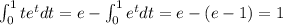
and

`\large \boxed{W=\int_(C)Fdr=e+24}`

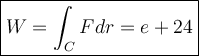
To show that F is not conservative, we could find another path D from A to B such that the work to move the particle from A to B along D is different to e+24

Now, let D be the path consisting on the segment that goes from A to (1,0,0) and then the segment from (1,0,0) to B.

The segment that goes from A to (1,0,0) can be parameterized as

r(t) = (t,0,0) with 0≤ t ≤ 1

so the work required to move the particle from A to (1,0,0) is

`\large \int_(0)^(1)(e^t,e^t,0)\circ (1,0,0)dt =\int_(0)^(1)e^tdt=e-1`

The segment that goes from (1,0,0) to B can be parameterized as

r(t) = (1-2t,2t,-5t) with 0≤ t ≤ 1

so the work required to move the particle from (1,0,0) to B is

`\large \int_(0)^(1)(e,e,-5et)\circ (-2,2,-5)dt =25e\int_(0)^(1)tdt=(25e)/(2)`

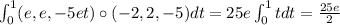
Hence, the work required to move the particle from A to B along D is

e - 1 + (25e)/2 = (27e)/2 -1

since this result differs from e+24, the force field F is not conservative.