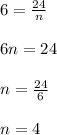Question

If g(n) varies inversely with n and g(n) = 8 when n = 3, find the value of n when g(n) = 6.

24
17
0
4

Answer 1

Answer: Last option.

Explanation:

By definition, Inverse variation equations have this form:

`y=(k)/(x)`

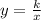
Where "k" is the constant of variation.

In this case, it is:

`g(n)=(k)/(n)`

Knowing that
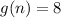`g(n) = 8` when
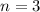`n = 3`, we can substitute values into the equation and solve for "k":

`8=(k)/(3)\\\\8*3=k\\\\k=24`

Therefore, we can find the value of "n" when
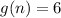`g(n) = 6` by substiuting this value and the value of "k" into the equation and solving for "n". Then:

`6=(24)/(n)\\\\6n=24\\\\n=(24)/(6)\\\\n=4`