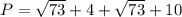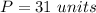Question

A trapezoid has coordinates of (-5, -3), (-2, 5), (2, 5), and (5, -3). What is the approximate perimeter of the trapezoid?

Round your answer to the nearest whole number (number that is not a decimal).

Answer 1

The approximate perimeter of the trapezoid is 31 units

Explanation:

step 1

Plot the trapezoid

Let

A(-5, -3), B(-2, 5), C(2, 5), and D(5, -3)

see the attached figure

step 2

Find the perimeter of trapezoid

we know that

The perimeter of trapezoid is equal to

`P=AB+BC+CD+AD`

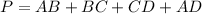
the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

Find the distance AB

we have

`A(-5, -3),B(-2, 5)`

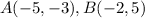
substitute in the formula

`d=\sqrt{(5+3)^(2)+(-2+5)^(2)}`

`d=\sqrt{(8)^(2)+(3)^(2)}`

`d_A_B=√(73)\ units`

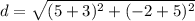
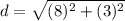
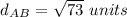
Find the distance BC

we have

`B(-2, 5),C(2, 5)`

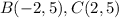
substitute in the formula

`d=\sqrt{(5-5)^(2)+(2+2)^(2)}`

`d=\sqrt{(0)^(2)+(4)^(2)}`

`d_B_C=4\ units`

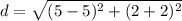
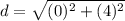
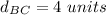
Find the distance CD

we have

`C(2, 5),D(5, -3)`

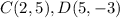
substitute in the formula

`d=\sqrt{(-3-5)^(2)+(5-2)^(2)}`

`d=\sqrt{(-8)^(2)+(3)^(2)}`

`d_C_D=√(73)\ units`

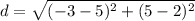
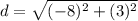
Find the distance AD

we have

`A(-5, -3),D(5, -3)`

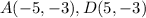
substitute in the formula

`d=\sqrt{(-3+3)^(2)+(5+5)^(2)}`

`d=\sqrt{(0)^(2)+(10)^(2)}`

`d_A_D=10\ units`

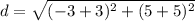
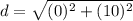
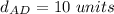
step 3

Find the perimeter

`P=AB+BC+CD+AD`

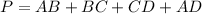
substitute the values

`P=√(73)+4+√(73)+10`

`P=31\ units`