Answer:
0.0004498
Explanation:
Let us define the events:
A = The test returns positive.
B = The accused was present.
Since everyone in the town has an equal probability of being at the murder scene, and the town has a population of 10,000
P(B) = 1/10000 = 0.0001
We have that the probability the test returning positive given that the accused was actually present at the scene is 0.9
P(A | B) = 0.9
and the probability that the test returns negative given that the accused was not present at the scene is 0.8
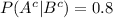
where
 are the complements of A and B respectively.
are the complements of A and B respectively.
We want to determine the probability that the DNA test returned a positive result given that the accused was at the murder scene, that is, P(B | A).
We know that P(A | B) = 0.9, so
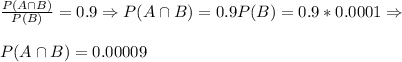
Now, we have
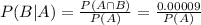
So if we can determine P(A), the result will follow.
By De Morgan's Law
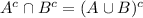
so
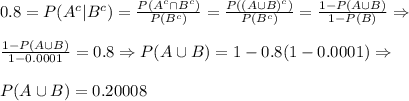
Using the formula
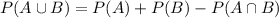
and replacing the values we have found

and finally, the desired result is
