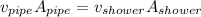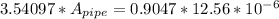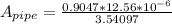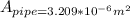To solve the problem it is necessary to apply the concepts related to the calculation of discharge flow, Bernoulli equations and energy conservation in incompressible fluids.
PART A) For the calculation of the velocity we define the area and the flow, thus
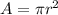
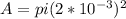
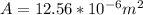
At the same time the rate of flow would be
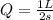
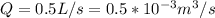
By definition the discharge is expressed as
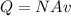
Where,
A= Area
v = velocity
N = Number of exits
Q = NAv
Re-arrange to find v,
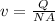
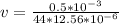
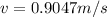
PART B) From the continuity equations formulated by Bernoulli we can calculate the speed of water in the pipe

Replacing with our values we have that
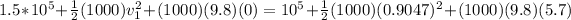

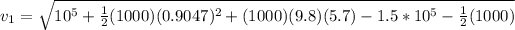

PART C) Assuming that water is an incomprehensible fluid we have to,