Answer:
The values are x = 0° or x = 60°
Explanation:
Given:
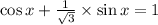
Let it be in the form of
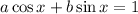 such that
such that
a = 1
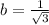
We have
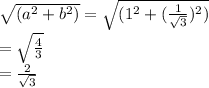
Now, Dividing both the side by
 we get
we get
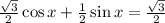
We Know
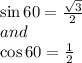
Now by replacing with above values we get
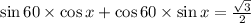
Also we have formula
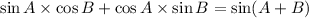
By applying the above Formula we get
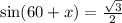
Also ,
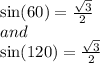
Comparing we get
60 + x = 60 or 60 + x = 120
∴ x = 0° ∴ x = 120 - 60 = 60°
Therefore, the values are x = 0° or x = 60° i.e between 0° to 360°