Question

Say that you are in a large room at temperature TC = 300 K. Someone gives you a pot of hot soup at a temperature of TH = 340 K. You set the bowl up so that as it cools to room temperature the heat first flows through a Carnot Engine. The soup has Cv= (33 J/K). Assume that the volume of the soup does not change. What fraction of the total heat QH that is lost by the soup can be turned into useable work by the engine? Work / QH =

Answer 1

To solve the problem it is necessary to take into account the concepts related to energy efficiency in the engines, the work done, the heat input in the systems, the exchange and loss of heat in the soupy the radius between the work done the lost heat ( efficiency).

By definition the efficiency of the heat engine is

`\epsilon = 1- (T_c)/(T_h)`

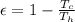
Where,

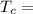`T_c =` Temperature at the room

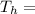`T_h  =`Temperature of the soup

The work done is defined as,

`dW = \epsilon(dQ_h)`

Where
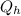`Q_h` represents the input heat and at the same time is defined as

`dQ_h =c_v (dT_h)`

Where,

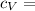`c_V =`Specific Heat

The change at the work would be defined then as

`dW = \epsilon(dQ_h)`

`dW = \epsilon c_v (dT_h)`

`dW = (1-(T_c)/(T_h))c_v (dT_h)`

`W = \int dW = \int (1-(T_c)/(T_h))c_v (dT_h)`

`W = c_v (T_h-T_c)-c_v T_c ln((T_h)/(T_c))`

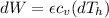
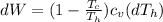
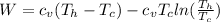
On the other hand we have that the heat lost by the soup is equal to

`dQ_h =c_v (dT_h)`

`Q_h =c_v (T_h-T_c)`

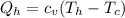
The ratio between both would be,

`(W)/(Q_h) = (c_v (T_h-T_c)-c_v T_c ln((T_h)/(T_c)))/(c_v (T_h-T_c))`

`(W)/(Q_h) = (1+ln((T_h)/(T_c)))/(1-(T_h)/(T_c))`

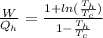
Replacing with our values we have,

`(W)/(Q_h) = 1+(ln((340K)/(300K)))/(1-(340K)/(300K))`

`(W)/(Q_h) = 0.0613`

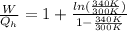
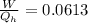
Therefore the fraction of heat lost by the soup that can be turned into useable work by the engine is 0.0613.