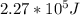Question

A school has installed a modestly-sized wind turbine. The three blades are 4.0 m long; each blade has a mass of 45 kg. You can assume that the blades are uniform along their lengths. Part A When the blades spin at 240 rpm, what is the kinetic energy of the blade assembly?

Answer 1

To solve the exercise it is necessary to apply the concepts related to kinetic energy by rotation and the moment of rotational inertia.

Rotational energy is defined as

`KE = (1)/(2)I\omega^2`

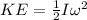
Where,

I = Inertia moment

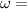`\omega =` Angular velocity

While the Rotational inertia of each blade is given as

`I = (1)/(3)ml^2`

Where,

m= mass

l = length

We have also that the assembly of the motor has three blade, then the total rotational inertia is

`I_m = 3*(1)/(3)ml^2`

`I_m = ml^2`

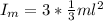
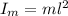
Replacing with our values

`I_m = 45*4^2`

`I_m = 720Kgm^2`

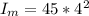
We have the angular velocity in rev per minute then in rad per second is

`\omega= 240rpm ((2\pi rad)/(1rev))((1min)/(60s))`

`\omega=25.13rad/s`

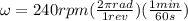
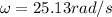
Then the total Kinetic Energy at the system is

`KE = (1)/(2)720*(25.13)^2`

`KE= 2.27*10^5J`

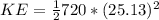
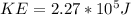
Therefore the total Kinetic Energy at the system is
`2.27*10^5J`