Question

There are 39 students in a psychology class. The class has been divided into 10 groups; 9 groups have 4 students in them, 1 group only has 3 students. The instructor puts all of the students names in a hat and then randomly draws 1 name. What are the chances that the one name will be the name of someone in the small, 3-person group?

Answer 1

Answer: Our required probability is 0.1875.

Explanation:

Since we have given that

Number of students = 39

Total Number of groups = 10

Number of groups containing 4 students = 9

Number of groups containing 3 students = 1

So, Probability of getting group of 4 students =
`(9)/(10)`

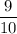
Probability of getting group of 3 students =
`(1)/(10)`

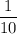
Using the "Bayes theorem":

Probability that the one name will be the name of someone in the small 3-person group is given by

`((1)/(10)* (3)/(39))/((1)/(10)* (3)/(39)+(9)/(10)* (4)/(39))\\\\=((3)/(390))/((3+13)/(390))\\\\=(3)/(16)\\\\=0.1875`

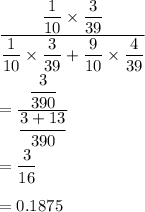
Hence, our required probability is 0.1875.