Answer: 52
Explanation:
Formula for sample size:-
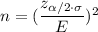
, where
 = population standard deviation.
= population standard deviation.
 = Two -tailed z-value for
= Two -tailed z-value for
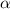 (significance level)
(significance level)
E= margin of error.
Given : tex]\sigma=\text{ 0.30 ounce}[/tex]
⇒Significance level for 99.6% confidence level :
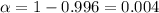
By using z-value table ,Two -tailed z-value for
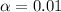 :
:
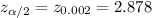
E= 0.12 ounces.
Minimum sample size will be :-
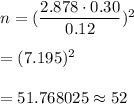
Hence, the minimum sample size for the number of packages the inspector must select = 52