Answer:
The total amount of the mortgage is $ 871879.4
Explanation:
Given as :
The cost of house = $ 175,000
The first 80% of mortgage amount = 80% of $ 175,000 = 140,000
The second 20 % of mortgage amount = 20% of $ 175,000 = 35,000
The rate of interest for 80 % mortgage = 4.75 %
The rate of interest for 20 % mortgage = 7.525 %
The time period for both mortgage is 30 years
Let The amount at 80 % mortgage =
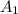
And The amount at 20 % mortgage =

So, From compounded method
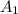 = principal ×
= principal ×
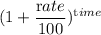
or,
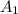 = 140,000 ×
= 140,000 ×
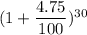
Or,
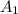 = 140,000 ×
= 140,000 ×

Or,
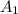 = 140,000 × 4.02365
= 140,000 × 4.02365
Or,
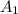 = $ 563311
= $ 563311
Again
 = principal ×
= principal ×
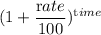
or,
 = 35,000 ×
= 35,000 ×
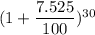
Or,
 = 35,000 ×
= 35,000 ×
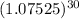
Or,
 = 35,000 × 8.81624
= 35,000 × 8.81624
Or,
 = $ 308568.4
= $ 308568.4
∴ Total amount A =
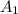 +
+

I.e A = $ 563311 + $ 308568.4 = $ 871879.4
Hence The total amount of the mortgage is $ 871879.4 answer