Question

From where the shoes spilled (48°N, 161°W) to where they were found on May 22nd 1996 (54°N, 133°W), how many kilometers did they travel?

How many days did they take to travel that distance (use April 30 as the date found)?

What was their rate of travel in kilometers per hour?

Answer 1

a) Around 2,052.583 Km.

b) Around 22 days.

c) Around 3.887 Km/h

Explanation:

a)

In order to find and approximation of the distance traveled, we have to make some assumptions:

• They traveled directly from the starting point to the end point without detours.
• There where no high hills or deep depressions between the points.

If these assumptions hold, then the distance d in Km can be calculated by using the haversine formula:

`\large d=2R*arcsin\left(√(sin^2((\varphi_2-\varphi_1)/2)+cos(\varphi_1)cos(\varphi_2)sin^2((\lambda_2-\lambda_1)/2))\right)`

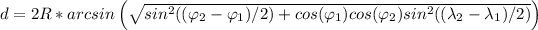
where

`\large (\varphi_1, \lambda_1)` are the latitude and longitude of the starting point in radians.

`\large (\varphi_2, \lambda_2)` are the latitude and longitude of the end point in radians.

R = radius of Earth in kilometers.

Be careful to convert the angles into radians before computing the trigonometric functions. This can be done by cross-multiplication knowing that 180° ≅ 3.141592654 radians.

In the problem we have

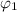`\large \varphi_1` = 48° = 0.837758041 radians

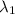`\large \lambda_1` = 161° = 2.809980096 radians

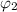`\large \varphi_2` = 54° = 0.942477796 radians

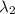`\large \lambda_2` = 133° = 2.321287905 radians

so

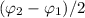`\large (\varphi_2-\varphi_1)/2` = 3° = 0.052359878 radians

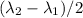`\large (\lambda_2-\lambda_1)/2` = -14° = -0.2443461 radians

Replacing in the formula for the distance:

`\large d=2R*arcsin\left(√(sin^2(0.052359878)+cos(0.837758041)cos(0.942477796)sin^2(-0.2443461))\right)=\\\\=0.32237835*R`

According to NASA, the radius of Earth at the poles is around 6,356 Km and at the equator is 6,378 Km.

Since they traveled around the middle point between the equator and the North pole, a better estimate of the radius in this case would be the average (6,378+6,356)/2 = 6,367 Km

We have that an approximation to the distance traveled would be

0.32237835*6,367 = 2,052.583 Km

b)

Assuming that the shoes where left and found the same year, there are 22 days from April 30th to May 22nd , so they traveled for around 22 days (this may vary slightly depending on the exact time the shoes were left and found)

c)

They traveled 2,052.583 Km in 22 days.

22 days equals 22*24 = 528 hours.

By cross-multiplication

528 h _______ 2,052.583 Km

1 h __________ x Km

x = 2,052.583/528 ≅ 3.887 Km

So they traveled at a rate of 3.887 Km/h