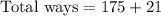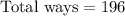Question

Suppose that 7 female and 5 male applicants have been successfully screened for 5 positions. If the 5 positions are filled at random from the 12 ​finalists, what is the probability of selecting

a. 3 females and 2 males?
b. 4 females and 1 male?
c. 5 females?
d. at least 4 females?

Answer 1

(a) 350

(b) 175

(c) 21

(d) 196

Explanation:

Number of females = 7

Number of males = 5

Total ways of selecting r items from n items is

`^nC_r=(n!)/(r!(n-r)!)`

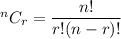
(a)

Total ways of selecting 3 females and 2 males.

`\text{Total ways}=^7C_3* ^5C_2`

`\text{Total ways}=(7!)/(3!(7-3)!)* (5!)/(2!(5-2)!)`

`\text{Total ways}=35* 10`

`\text{Total ways}=350`

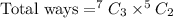
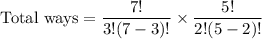
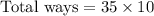
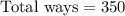
(b)

Total ways of selecting 4 females and 1 male.

`\text{Total ways}=^7C_4* ^5C_1`

`\text{Total ways}=32* 5`

`\text{Total ways}=175`

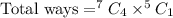
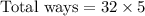
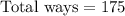
(c)

Total ways of selecting 5 females.

`\text{Total ways}=^7C_5* ^5C_0`

`\text{Total ways}=21* 1`

`\text{Total ways}=21`

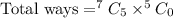
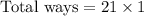
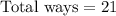
(d)

Total ways of selecting at least 4 females.

Total ways = 4 females + 5 females

`\text{Total ways}=175+21`

`\text{Total ways}=196`