Question

Trainees must complete a specific task in less than 2 minutes. Consider the probability density function below for the time it takes a trainee to complete the task.f(x) = 0.85 - 0.35x0 < x < 2a) What is the probability a trainee will complete the task in less than 1.31 minutes? Give your answer to four decimal places.b) What is the probability that a trainee will complete the task in more than 1.31 minutes? Give your answer to four decimal places.c) What is the probability it will take a trainee between 0.25 minutes and 1.31 minutes to complete the task? Give your answer to four decimal places.d) What is the expected time it will take a trainee to complete the task? Give your answer to four decimal places.e) If X represents the time it takes to complete the task, what is E(X2)? Give your answer to four decimal places.f) If X represents the time it takes to complete the task, what is Var(X)? Give your answer to four decimal places.

Answer 1

a) 0.8132 or 81.32%

b) 0.1868 or 18.68%

c) 0.6116 or 61.16%

d) 0.7667 minutes

e) 0.8667 minutes

f) 0.1 minutes

Explanation:

a)

If f(x) = 0.85-0.35x (0<x<2) is the PDF and X is the random variable that measures the time it takes for a trainee to complete the task, the probability a trainee will complete the task in less than 1.31 minutes is P(X<1.31)

`\large P(X<1.31)=\int_(0)^(1.31)f(x)dx=\int_(0)^(1.31)(0.85-0.35x)dx=\\\\=0.85\int_(0)^(1.31)dx-0.35\int_(0)^(1.31)xdx=\\\\=0.85*1.31-0.35*((1.31)^2)/(2)=0.8132`

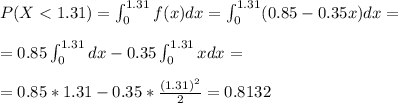
b)

The probability that a trainee will complete the task in more than 1.31 minutes is

P(X>1.31) = 1 - P(X<1.31) = 1 - 0.8132 = 0.1868

c)

The probability it will take a trainee between 0.25 minutes and 1.31 minutes to complete the task is P(0.25<X<1.31)

`\large P(0.25<X<1.31)=\int_(0.25)^(1.31)f(x)dx=\int_(0)^(1.31)f(x)dx-\int_(0)^(0.25)f(x)dx=\\\\=0.8132-\int_(0)^(0.25)(0.85-0.35x)dx=0.8132-0.85\int_(0)^(0.25)dx+0.35\int_(0)^(0.25)xdx=\\\\=0.8132-0.85*0.25+0.35*((0.25)^2)/(2)=0.6116`

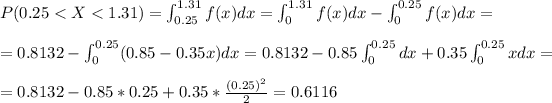
d)

the expected time it will take a trainee to complete the task

is E(X)

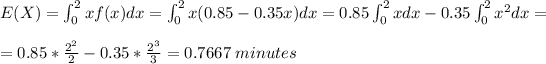
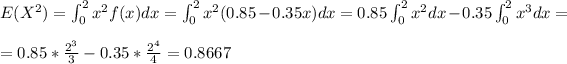
`\large E(X)=\int_(0)^(2)xf(x)dx=\int_(0)^(2)x(0.85-0.35x)dx=0.85\int_(0)^(2)xdx-0.35\int_(0)^(2)x^2dx=\\\\=0.85*(2^2)/(2)-0.35*(2^3)/(3)=0.7667\;minutes`

e)

`\large E(X^2)=\int_(0)^(2)x^2f(x)dx=\int_(0)^(2)x^2(0.85-0.35x)dx=0.85\int_(0)^(2)x^2dx-0.35\int_(0)^(2)x^3dx=\\\\=0.85*(2^3)/(3)-0.35*(2^4)/(4)=0.8667`

f)

`\large Var(X)=E(X^2)-(E(X))^2=0.8667-0.7667=0.1000`