Answer:
The probability of Rolling a 5 or a number greater than 3 is 0.5
The probability of Rolling a number less than 4 or an even number is 0.833
The probability of Rolling a 4 or an odd number is 0.667
Explanation:
Consider the provided information.
You roll a six-sided die.
The number of possible outcomes are: S={1, 2, 3, 4, 5, 6}
Part (a) Rolling a 5 or a number greater than 3.
Number greater than 3 are 4, 5 and 6.
A = {4,5,6}
The required probability is:

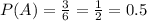
The probability of Rolling a 5 or a number greater than 3 is 0.5
Part (b) Rolling a number less than 4 or an even number.
Less than 4: {1,2,3}
Even numbers: {2,4,6}
Rolling a number less than 4 or an even number: B={1,2,3,4,6}
The required probability is:

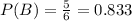
The probability of Rolling a number less than 4 or an even number is 0.833
Part (c) Rolling a 4 or an odd number.
Rolling a 4: {4}
Rolling an odd number: {1,3,5}
Rolling a 4 or an odd number: C={1,3,4,5}
The required probability is:
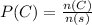
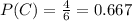
The probability of Rolling a 4 or an odd number is 0.667