Question

A line contains the points (10,7) and (10,-8). Write the equation of the line

Answer 1

Given two points
`(x_1, y_1)` and
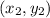`(x_2, y_2)`, the equation of the line passing through them is

`(x-x_2)/(x_1-x_2)=(y-y_2)/(y_1-y_2)`

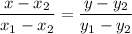
This formula, however, only works if the points don't share any of the two coordinates. Otherwise, one of the two conditions is true:

`x_1=x_2,\quad y_1=y_2`

And at least one of the denominators in the formula above will vanish.

So, if two points share the same x coordinate, they lie on the vertical line x=k, where k is the shared x coordinate.

Similarly, if two points share the same y coordinate, they lie on the horizontal line y=k, where k is the shared y coordinate.

In your case, the x coordinate is the same, so the points lie on the vertical line x=10.