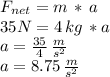Answer:
a. See attached diagram
b. There is no vertical motion
c. Net horizontal force: 35 N
d. Total net force: 35 N
e. Acceleration of the book: 8.75 m/s^2
Step-by-step explanation:
Please see attached diagram for all the forces acting on the book:
Forces acting vertically:
1) The book's weight (force exerted by gravity) is pictured in purple pointing down and labeled "w".
2) The normal force the table exerts on the book as reaction, is pictured in blue pointing up, and labeled "n". It cancels with the force of gravity, so there is no vertical movement since gravitational force and the normal are the only forces acting in the vertical direction.
Forces acting horizontally:
1) the pushing 50 N force is pictured in green and pointing to the right, parallel to the surface of the table.
2) the 15 N force of friction is pictured in red, and acting in opposite direction to the pushing force. It is represented by a shorter vector than the pushing force due to the fact that its magnitude is smaller.
In this horizontal direction there is a net force that is propelling the object in horizontal motion. This net force is the difference between the 50 N force and the 15 N force, resulting in a 35 N force pointing in the same direction as the pushing force.
The net horizontal force is 35 N in magnitude.
The addition of all forces acting is dominated by the horizontal components, since the vertical acting forces cancel each other. Therefore, the total net force acting on the book is the 35 N resulting horizontal force.
The acceleration of the book can be calculated via Newton's second law of motion: