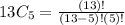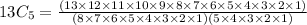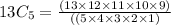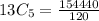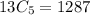Suppose that 5 out of 13 people are to be chosen to go on a mission trip. In how many ways can these 5 be chosen if the order in which they are chosen is not important.

Question

asked Nov 27, 2020 162k views

1 Answer

Tushar Saha · Answer 1 · 2020-12-01T23:42:10+0000

5 People can be chosen in 1287 ways if the order in which they are chosen is not important.

Explanation:

Given:

Total number of students= 13

Number of Students to be selected= 5

To Find :

The number of ways in which the 5 people can be selected=?

Solution:

Let us use the permutation and combination to solve this problem

nCr=((n)!)/((n-r)!(r)!)

So here , n =13 and r=5 ,

So after putting the value of n and r , the equation will be

13C_5=((13)!)/((13-5)!(5)!)

13C_5=((13 *12 *11 *10 *9 *8*7 *6 *5 *4 *3 *2 *1))/((8 *7 *6 *5 *4 *3 *2 *1)(5 *4 *3 *2 *1))

13C_5=((13 *12 *11 *10 *9 ))/(((5 *4 *3 *2 *1))

13C_5=(154440)/(120)

13C_5= 1287