Answer:
3.6 kHz
Step-by-step explanation:
The auditory canal is a closed pipe because it has one closed end, the end terminated at the eardrum.
The length of the first harmonic of a closed pipe is given as;
L = λ/4 -------------------- (i)
where L = Length
and λ = wavelength
2.4 = λ/4
λ = 2.4 x 4 = 9.6 cm
Also, v = fλ ------------------ (ii)
where v = speed of sound in air = 344 m/s
f = frequency of wave in Hertz
f = v/λ ------------------ (iii)
convert 9.6 cm to m = 0.096 m
substitute for λ and v in (iii)
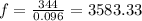
3583.33 Hz = 3600 Hz = 3.6 kHz