Question

Select the function that matches the graph.

y = 3x
y = 3x2 + 1
y = 3x - 1
y = 3x + 1

Answer 1

the first one goes through (0,0) ||||||| the second is an exponential function so it goes through (0,1) and in a u shape going up ||||||| The third goes through (0,-1) ||||||||| The fourth goes through (0,1)

Explanation:

these are identifiein traits so you can find wich one the graph corresponds to since u never gave us a graph.

Answer 2

The graph is missing, but we can draw and describe each option.

Choice 1

`y=3x`

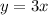
This is a linear function which passes throuhg the origin of the coordinate system because it doesn't have the constant
`b` which is the y-intercept of the line.

The first image attached shows this function.

Choice 2

`y=3x^(2) +1`

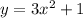
This is a quadratic function. Its graph belongs to a parabola, all quadratic functions are represented by a parabola. In this case, the parabola has a vertex at (0,1). The second image attached shows this function.

Choice 3

`y=3x-1`

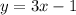
This is also a linear function, which is parallel to the first function, because they have the same slope of 3. But this one has y-intercept at (0,-1). The third image attached shows this function.

Choice 4

`y=3x+1`

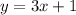
This is also a linear function parallel to function 1 and function 3. The fourth image attached shows its graph. In this case, the line has y-intercept at (0,1).