There is a typo error, the perimeter of equilateral triangle ABC is 81/√3 centimeters.
Answer:
Radius = OB= 27 cm
Apothem = 13.5 cm
A diagram is attached for reference.
Explanation:
Given,
The perimeter of equilateral triangle ABC is 81/√3 centimeters.
Substituting this in the formula of perimeter of equilateral triangle =
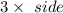
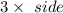
![=[tex]81√(3)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jgo3zvf85rmis1a1sm56nxfjo7kf60pn5y.png)
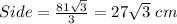
Thus from the diagram , Side
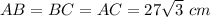
We know each angle of an equilateral triangle is 60°.
From the diagram, OB is an angle bisector.
Thus
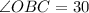 °
°
Apothem is the line segment from the mid point of any side to the center the equilateral triangle.
Therefore considering ΔOBE, and applying tan function.
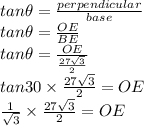
Thus ,apothem OE= 13.5 cm
Now for radius,
We consider ΔOBE
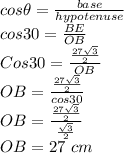
Thus for
Perimeter of equilateral triangle ABC is 81/√3 centimeters,
The radius of equilateral triangle ABC is 27 cm
The apothem of equilateral triangle ABC is 13.5 cm