Question

9/20

Find the number of real number solutions for the equation. x2 + 5x + 7 = 0
nd
01
ations
02
O cannot be determined
are
00
e
100%

Answer 1

Question:

Find the number of real number solutions for the equation. x^2 + 5x + 7 = 0

Answer:

The number of real solutions for the equation
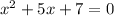`x^(2)+5 x+7=0` is zero

Solution:

For a Quadratic Equation of form :
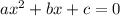`a x^(2)+b x+c=0` ---- eqn 1

The solution is
`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

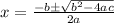
Now , the given Quadratic Equation is
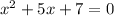`x^(2)+5 x+7=0` ---- eqn 2

On comparing Equation (1) and Equation(2), we get

a = 1 , b = 5 and c = 7

In
`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}` ,
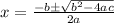`b^2 - 4ac` is called the discriminant of the quadratic equation

Its value determines the nature of roots

Now, here are the rules with discriminants:

1) D > 0; there are 2 real solutions in the equation

2) D = 0; there is 1 real solution in the equation

3) D < 0; there are no real solutions in the equation

Now let solve for given equation

`D= b^2 - 4ac\\\\D = 5^2 - 4(1)(7)\\\\D = 25 - 28 \\\\D = -3`

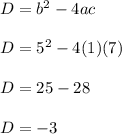
Since -3 is less than 0, this means that there are 0 real solutions in this equation.