Answer:
The required point is, (7, -2)
Explanation:
The straight line passing through (0,0) and (2,7) is,
y =
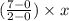
⇒ y = 3.5x --------------(1)
Now, the straight line perpendicular to this line and passing through (0, 0) is
y =
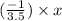
⇒ 7y + 2x = 0 -------------(2)
Let, (h,k) be the required point.
then, it is on the line 7y + 2x = 0
⇒7k + 2h = 0
⇒k =
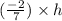 ------------(3)
------------(3)
Again, distance from (0,0) of (h, k) is same as that of (2,7)
⇒
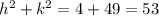
⇒
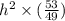 = 53 [putting the value of k from (3)]
= 53 [putting the value of k from (3)]
⇒
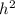 = 49
= 49
⇒h = 7 [since, (h,k) is in 4th quadrant, so,h >0]
So, k = -2 [putting the value of h in (3)]
So, the required point is, (7, -2)