Question

9/20

Find the number of real number solutions for the equation. x2 + 5x + 7 = 0
nd
01
ations
02
O cannot be determined
are
00
e
100%

Answer 1

No real roots

Explanation:

The given quadratic equation is

`{x}^(2) + 5x + 7 = 0`

Comparing this to the general quadratic equation:

`a {x}^(2) + bx + c = 0`

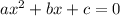
We have a=1, b=5 and c=7

Recall that the discriminant is

`D = {b}^(2) - 4ac`

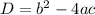
We plug in the values to get:

`D = {5}^(2) - 4(1)(7)`

`D =25- 28 = - 3`

Since the discriminant is less than zero, the given equation has no real roots