Question

ASAP PLEASE PLEASE HELP The measured dimensions of a rectangle are 6 m by 4 m to the nearest whole unit. Find the minimum and maximum possible areas of the rectangle.

Answer 1

The minimum possible area of the rectangle is 19.25 m² and the maximum possible area is 29.25 m².

Step-by-step explanation:

To find the minimum and maximum possible areas of the rectangle, we need to consider the possible values that the length and width can take.

Given that the measured dimensions are 6 m by 4 m to the nearest whole unit, the minimum possible length would be 5.5 m (6 m - 0.5 m) and the minimum possible width would be 3.5 m (4 m - 0.5 m).

Similarly, the maximum possible length would be 6.5 m (6 m + 0.5 m) and the maximum possible width would be 4.5 m (4 m + 0.5 m).

To calculate the minimum and maximum possible areas, we multiply the minimum and maximum possible lengths by the minimum and maximum possible widths respectively. The minimum possible area would be 5.5 m x 3.5 m = 19.25 m² and the maximum possible area would be 6.5 m x 4.5 m = 29.25 m².

Answer 2

The minimum possible area of the rectangle is 19.25 m² and the maximum possible area of the rectangle is 29.25 m².

Step-by-step explanation:

Given:

The dimensions of rectangle are 6m by 4m.

Now, to find the minimum and the maximum possible areas.

So, for the minimum area the dimensions would be 5.5m by 3.5m.

Now, by putting the formula of finding the area:

Area = 5.5m by 3.5m

`Area = 19.25 m^(2)`

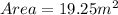
Now, for the maximum area we again put the formula and the dimensions would be 6.5m by 4.5m:

Area = 6.5m by 4.5m

`Area = 29.25m^(2)`

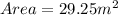
Therefore, the minimum possible area of the rectangle is 19.25 m² and the maximum possible area of the rectangle is 29.25 m².