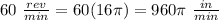Question

A belt runs a pulley of radius 8 inches at 60 revolutions per minute. a) Find the angular speed in radians per minute. b) Find the linear speed in inches per minute.

Answer 1

Part a)
`120\pi\ (rad)/(min)`

Part b)
`960\pi\ (in)/(min)`

Explanation:

we have

60 rev/min

Part a) Find the angular speed in radians per minute

we know that

One revolution represent 2π radians (complete circle)

so

`1\ rev=2\pi \ rad`

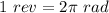
To convert rev to rad, multiply by 2π

`60\ (rev)/(min)=60(2\pi)=120\pi\ (rad)/(min)`

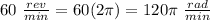
Part b) Find the linear speed in inches per minute

we know that

The circumference of a circle is equal to

`C=2\pi r`

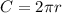
we have

`r=8\ in` ----> given problem

substitute

`C=2\pi(8)`

`C=16\pi\ in`

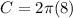
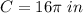
Remember that

One revolution subtends a length equal to the circumference of the circle

so

`1\ rev=16\pi\ in`

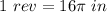
To convert rev to in, multiply by 16π

`60\ (rev)/(min)=60(16\pi)=960\pi\ (in)/(min)`