Answer:
The speed of the boat in still water is 12 km/hour.
Explanation:
Given:
Boat goes 50 km downstream and 30 km upstream. The speed of the stream 3 km/hour.
Now, to find the speed of the boat in still water:
Let the speed of boat in still water be
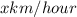 .
.
The speed of the downstream be
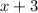
And, the speed of the upstream be
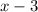
And, now we find the time by putting the formula:
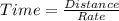
So, downstream time is:
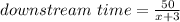
So, upstream time is:
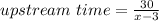
According to question:
Time upstream = Time downstream
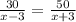
By cross multiplication:
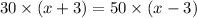
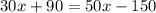
By taking variables in one side and taking numbers on the other side we get:
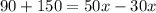
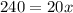
Dividing both sides by 20 we get :
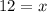
Therefore, the speed of the boat in still water is 12 km/hour.