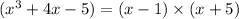Question

Find all of the zeros and write a linear factorization of the function f(x)=x^3+4x-5

Answer 1

The given polynomial f(x) can be factorized as
`(x^3+4x-5) = (x-1) *  (x +5)`

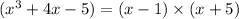
Explanation:

Here, the given function is:
`f(x)=x^3+4x-5`

Now If we try and put any arbitrary value say x = 1, we get

`f(1)=(1)^3+4(1)-5  = 5- 5  = 0` , or f(1) = 0

⇒ x =1 is the zero of the given polynomial.

⇒ (x-1) is the ROOT of the Polynomial.

Now, dividing the polynomial, with this root, we get:

`(x^3+4x-5)/((x-1))  = (x +5)\\\implies  (x^3+4x-5) = (x-1) *  (x +5)`

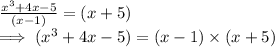
⇒ (x+5) is the another ROOT of the Polynomial.

So, the given polynomial p(x) has two zeroes 1 and -5.

Hence, the given polynomial f(x) can be factorized as
`(x^3+4x-5) = (x-1) *  (x +5)`