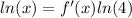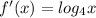Answer:
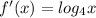
Explanation:
Lets first identify the function using the given data.
Clearly we can see the trend in the data.
The value of the function
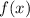 is
is
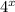
So,
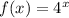
Now we find the inverse of the function.
Let
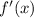 be the inverse function.
be the inverse function.
Now substitute
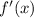 in the place of
in the place of
 and
and
 in the place of
in the place of
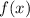 in the above equation.
in the above equation.
So,
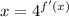
Applying logarithm on both sides,