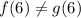Answer:
f(3) = g(3)
Explanation:
we know that
When solve a system of linear equations by graphing, the solution of the system is the intersection point both lines
The intersection point is common point for bot lines
In this problem
we have the system of equations
f(x)
g(x)
The intersection point is (3,6)
That means that the solution for the system is the point (3,6)
so
For x=3
The value of f(3)=6 and the value of g(3)=3
therefore
f(3)=g(3)
Verify the statements
Find the equation of the blue line f(x)
(0,-3) and (1,0)
the slope is
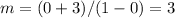
The equation in slope intercept form is equal to
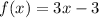
Find the equation of the red line g(x)
(-3,0) and (0,3)
the slope is

The equation in slope intercept form is equal to
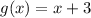
case 1) f(6) = g(3)
The statement is false
Because
For x=6 ----->

For x=3 ---->
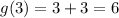
therefore
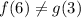
case 2) f(3) = g(3)
The statement is true
Because
For x=3 ----->
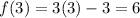
For x=3 ---->
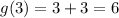
therefore
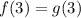
case 3) f(3) = g(6)
The statement is false
Because
For x=3 ----->
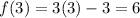
For x=6 ---->
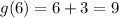
therefore
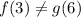
case 4) f(6) = g(6)
The statement is false
Because
For x=6 ----->

For x=6 ---->
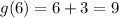
therefore