The average rate of change of d(t) from t = 3 to t = 6 represent: A. The coin travels an average distance of 44.1 meters from 3 seconds to 6 seconds.
In Mathematics and Geometry, the average rate of change (ARoC) of a function f(x) on a closed interval [a, b] can be calculated by using this mathematical equation (formula):
Average rate of change (ARoC) =
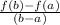
Based on the given quadratic function, we can reasonably infer and logically deduce the following:
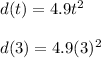
f(a) = d(3) = 44.1
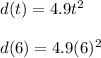
f(a) = d(3) = 176.4
Next, we would determine the average rate of change (ARoC) of the function over the interval [3, 6]:
Average rate of change (ARoC) =
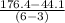
Average rate of change (ARoC) = 44.1 meters.
In this context, we can logically deduce that the coin travels an average distance of 44.1 meters from 3 seconds to 6 seconds.