Answer:
39.6 m
Explanation:
See the attached diagram.
Let AB is the height of the tree and CD is the height of the council arborist.
So, we have to determine AB while CD is given to be 1.8 m.
If the position of the sun at the time is such that the inclination of ray of light is x Degrees, then the shadow of the arborist is CE = 1.5 m and the shadow of the tree is AE = 33 m {Given}
As Δ ABE and Δ CDE are similar triangles, so, we can write
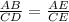
⇒
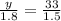
⇒ y = 39.6 m
Hence, the height of the tree is 39.6 m. (Answer)