Question

What is the area of a regular pentagon with a side of 10in?

Answer 1

Area of a regular pentagon with a side of 10in is 172

Explanation:

Given:

Side of the regular pentagon = 10in

To Find:

Area of the regular pentagon=?

Solution:

We know that ,

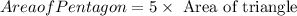`Area of Pentagon = 5*\text{ Area of triangle}`................(1)

Step 1: Finding the Area of the triangle

we know that in a right angle triangle, there are base, height and hypotenuse
`tan((\pi)/(5)) =( height)/(hypotenuse )`

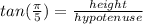
So, from the above equation,

`height=((base/2))/(tan(36^(\circ)))`

`height=(5)/(tan(36))=6.88`

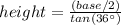
area of right angle triangle

=>
`(1)/(2)* base * height`

=>
`=(1)/(2) * 5* 6.88`

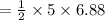
=> 17.20

Area of the triangle =2 x area of right angle triangle

Area of the triangle =2 x 17.20

Area of the triangle= 34.40

Step 2: Finding the Area of the pentagon

Substituting the values in (1)

`Area of Pentagon = 5* 34.40`

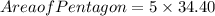
Area of Pentagon= 172