Question

There are 10 true-false questions and 20 multiple choice questions from which to choose a five-question quiz how many ways can the quiz be selected if there must be at least three multiple choice questions selected?​

Answer 1

In 68229 ways can the quiz be selected such that there is atleast three multiple choice questions

Explanation:

Given:

Number of True or false questions= 10

Number of multiple choice questions= 20

To Find:

How many ways can 5 questions can be selected if there must be at least three multiple choice questions =?

Solution:

Combination

A combination is a mathematical technique that determines the number of possible arrangements in a collection of items where the order of the selection does not matter. In combinations, you can select the items in any order.

The question States there sholud be ATLEAST 3 multiple choice question,

So, we may have

(3 Multiple choice question and 2 true or false question) or

(4 Multiple choice question and 1 true or false question) or

(5 Multiple choice question and 0 true or false question)

Required Number of ways = (20C3 X10C2) +(20C4 X10C1) + (20C5 X10C0)

Required Number of ways
`=((20!)/(20!(20-3)!)*(10!)/(10!(10-2)!))+((20!)/(20!(20-4)!) * (10!)/(10!(10-1)!)) +((20!)/(20!(20-4)!) * (10!)/(10!(10-0)!))`

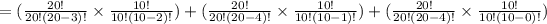
Required Number of ways = ( 1140 x 42) + (4845 x 10) +(15504 x 1)

Required Number of ways = 47880+48450+15504

Required Number of ways = 68229