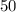Question

Rozwiąż podane przykłady. Oblicz miary kątów ..

Daje naj

Answer 1

α= 22°

β= 100°

Y= 50°

Explanation:

Given are three different triangles,

In the first triangle, two of the angles are 38° and α° and the third angle would be 120°(using vertical opposite angle equal property).

We know sum of all three angles of a triangle
`=180`°

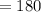Substituting,

`\alpha +38+120=180\\\alpha +158=180\\\alpha =180-158\\\alpha =22`

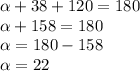
Similarly,

In the second triangle, two of the angles are 40° and 60° and the the angle we have to find is outside(β).

We know the outside angle is equal to the sum of opposite inside angles of a triangle.

Therefore,

β
`=40+60\\=100`

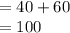
In third triangle,'Y' is inside angle of the triangle and 70° and 160° are outside.

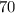`70`° makes linear pair,

sum of linear pair angles=
`180`°

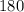Therefore the angle of triangle next to
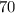`70`° would be
`180-70=110`°

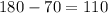We see 'Y' is outside and opposite to both the inside angles
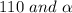`110 \ and \ \alpha`. thus applying the property,

`Y + 110 = 160\\Y=160-110\\Y=50`°

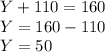Therefore 'Y' =
`50`