Answer:
A ) a = 8
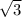 , c = 8
, c = 8
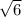
B ) a = 2
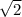 , b = 2
, b = 2
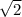
Explanation:
Given as :
A ) ABC is right triangle , right angle at c
So, ∠ C = 90°
And ∠ A = 45° , ∠ B = 45°
And BC = a , CA = b , AB = c
measure of side b = 8
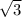
Now, from right angle triangle ABC
Tan ∠ C =
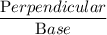
Or, Tan 45° =
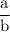
or, 1 =
![\frac{\textrm a}{\textrm8[tex]√(3)]() }[/tex]
}[/tex]
∴ a = 8
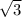
Now, c² = a² + b²
Or, c² = ( 8
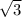 )² + (8
)² + (8
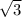 )²
)²
Or, c = 8
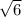
Again
B ) c = 4
So, Sin ∠ A =
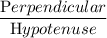
or , Sin 45° =

Or , a = 4 × Sin 45°
∴ a = 4 ×
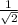
I.e a = 2
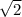
Now , b² = c² - a²
Or, b² = 4² - (2
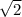 )²
)²
Or, b² = 16 - 8 = 8
Or , b = 2
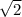
Hence the solution of given expression
A ) a = 8
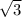 , c = 8
, c = 8
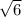
B ) a = 2
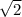 , b = 2
, b = 2
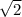 Answer
Answer